Nash Equilibria and Optimal Strategy for a Game I Just Made Up
I thought of a rather simple game which I gave the uninspired name “chip game” and have been wondering about the probabilities behind different strategies. The game goes like this
Take a board with N spaces. The defending player has D chips which they place in secret on these N spaces. The attacking player then places A chips on the board as well, without knowing where any of the defending chips have been placed. After this all placements are revealed and the attacking player wins if there is a single space on the board where they have more chips than the defender, otherwise the defender wins.
Thematically I thought about the case where an attacking force only needs to break through on a single point, while the defender can’t afford to loose a single position. What I wondered though was how to make this game somewhat fair, what would the probability for each player to win be with different strategies and different values of $N$, $D$, and $A$.
A few limiting cases put bounds on this
- if $A > D$ then the attacking player always wins by putting all chips on a single space, while the defending player cannot possibly stop them
- if $D > N \cdot A$ then the defending player always wins. By splitting their chips evenly no space will be left uncovered and even a concentrated attack will be unable to take any space
- giving either player more chips will never cause their chance to win to go down, having more is always advantageous
Based on this I considered a few potential strategies
- the attacker could go all in on a single space, knowing that they loose ties and only need to take 1 perhaps this could maximize their odds
- a defender which knows that the attacker is doing this could place $A$ chips on as many spaces as they can to hope to catch out this single attack
- conversely the attacker could spread their chips out, most likely loosing on any space which the defender has covered, but instead hoping to catch out a space with no defense
- interestingly this would have a 100% win rate against the defender using the previous strategy
- however if a defender knew this was coming they could most likely spread their chips out as well, and likely having more chips and winning ties means this would be a pretty good counter
- the attacker could do something in between, stacking most of their chips on a single spot to try to overwhelm a spread out defense, but also tossing a few random chips here and there to try to chance on an undefended space
All of this however leads back to one central question, “how can you find the probability of winning in a game with imperfect information and a wide range of strategies?”
What I settled on was looking at Nash equilibria as being representative of “optimal play”, and then finding out the win rates of both players at equilibrium. I worked this out in a jupyter notebook with a fun interactive plot, although its main purposes ended up being writing the input files for a command line Nash equilibrium utility called gambit.
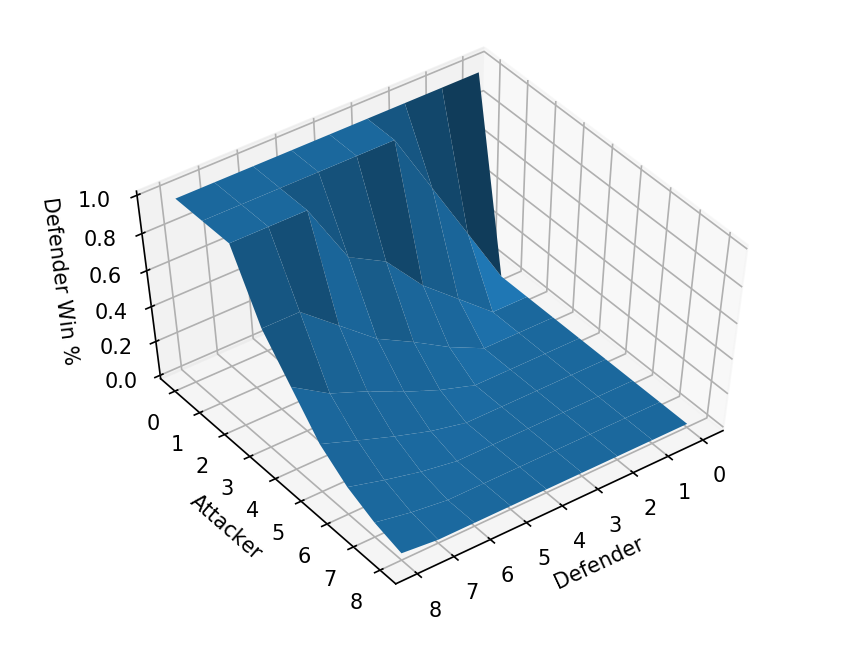
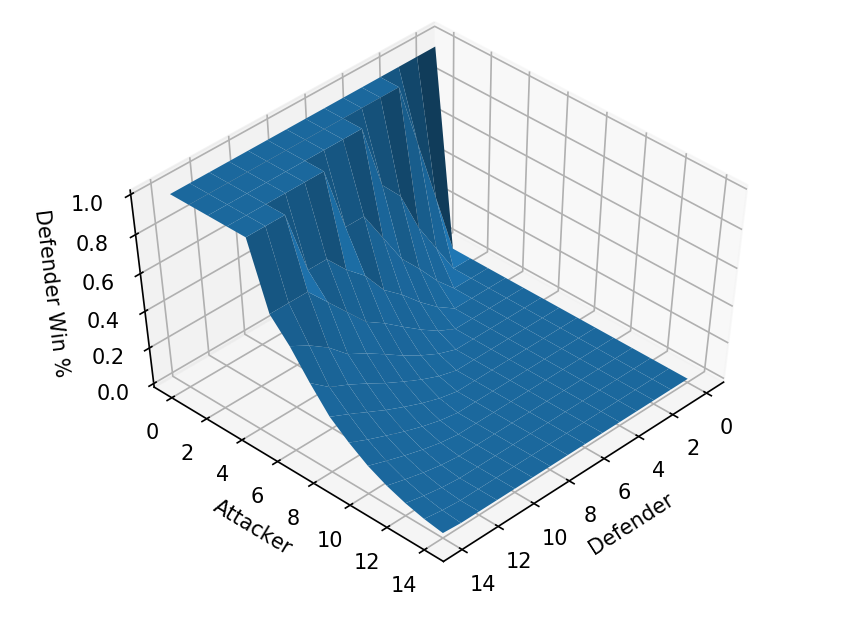
Here we can see some plots of the win rates for various values of $A$ and $D$. Up top is the plateau of our $D > N \cdot A$ limiting condition, while at the bottom of the cliff there is the region where the attacker always wins following the $A=D$ line.
What I didn’t expect was how smooth these graphs look, I was initially guessing that there would be quite a few more jagged edges along the win cliff representing various break even points. I also filled up pages and pages of 17x11’’ paper with tiny numbers to look at the different strategies. Overall it seems as if the fairly middle of the road strategies are the ones which form the Nash equilibria, with a win chance that is generally polynomial (due to how the combinatorics work out).
I think next it might be interesting to try playtesting the game some to see how it works out in practice, but overall fairly satisfied with what I found out about the probabilities involved.